6. Compare MMs or AMCEs between the subgroups • projoint

A key quantity of interest in conjoint tasks is whether estimates (MMs or AMCEs) differ across sub-populations. These subgroup comparisons are especially susceptible to IRR-induced measurement error bias. In the following, we present some sample codes so that researchers and adopt-and-modify them flexibly.

6.1 Load the projoint package.

Also load some additional packages required for this vignette

library(projoint)
library(dplyr)
library(ggplot2)

6.2 Profile-level analysis

Read and Wrangle data

To begin, define the outcome questions in the original dataset.

outcomes <- paste0("choice", seq(from = 1, to = 8, by = 1))
outcomes <- c(outcomes, "choice1_repeated_flipped")

Let’s make three data frames – the first data frame for the baseline group (in this example, respondents who did not report their race as “white”); he second data frame for the comparison group (in this example, respondents who reported their race as “white”), and the third data frame for both groups. Note that the .covariates argument should be specified in the reshape_conjoint() function for the third group.

# Pre-processing
df <- exampleData1 %>% 
  mutate(white = ifelse(race == "White", 1, 0))

df_0 <- df %>% 
  filter(white == 0) %>% 
  reshape_projoint(outcomes)

df_1 <- df %>% 
  filter(white == 1) %>% 
  reshape_projoint(outcomes)

df_d <- df %>% 
  reshape_projoint(outcomes, .covariates = "white")

Then, add and re-order the labels (see 2.3 Arrange the order and labels of attributes and levels).

df_0 <- read_labels(df_0, "temp/labels_arranged.csv")
df_1 <- read_labels(df_1, "temp/labels_arranged.csv")
df_d <- read_labels(df_d, "temp/labels_arranged.csv")

Estimate MMs or AMCEs and the difference in the estimates

For each of the three data frames, estimate the MMs, AMCEs, or the differences in these estimates. The following example estimate profile-level marginal means (default).

out_0 <- projoint(df_0)
out_1 <- projoint(df_1)
out_d <- projoint(df_d, .by_var = "white")

Importantly, if your conjoint design includes the repeated task, the projoint() function applied to each subgroup will estimate IRR for the corresponding subgroup. The output of out_d includes the data for these differences

out_d@estimates

## # A tibble: 48 × 11
##    estimand  att_level_choose estimate_1   se_1   tau estimate_0   se_0 estimate
##    <chr>     <chr>                 <dbl>  <dbl> <dbl>      <dbl>  <dbl>    <dbl>
##  1 mm_uncor… att1:level1           0.586 0.0157 0.158      0.545 0.0258   0.0401
##  2 mm_corre… att1:level1           0.625 0.0236 0.158      0.579 0.0433   0.0464
##  3 mm_uncor… att1:level2           0.480 0.0158 0.158      0.496 0.0250  -0.0163
##  4 mm_corre… att1:level2           0.471 0.0233 0.158      0.494 0.0432  -0.0229
##  5 mm_uncor… att1:level3           0.439 0.0153 0.158      0.460 0.0254  -0.0210
##  6 mm_corre… att1:level3           0.411 0.0227 0.158      0.431 0.0446  -0.0200
##  7 mm_uncor… att2:level1           0.529 0.0154 0.158      0.510 0.0245   0.0195
##  8 mm_corre… att2:level1           0.543 0.0226 0.158      0.517 0.0425   0.0260
##  9 mm_uncor… att2:level2           0.500 0.0157 0.158      0.461 0.0248   0.0394
## 10 mm_corre… att2:level2           0.500 0.0230 0.158      0.432 0.0417   0.0683
## # ℹ 38 more rows
## # ℹ 3 more variables: se <dbl>, conf.low <dbl>, conf.high <dbl>

You can also check tau for each subgroup:

out_d@tau

##        tau1      tau0
## 1 0.1582662 0.2113249

Then, make and save three ggplot objects.

plot_0 <- plot(out_0)
plot_1 <- plot(out_1)
plot_d <- plot(out_d, .by_var = TRUE)

Visualize subgroup differences

Then, make a plot using the patchwork package. Researchers can add/modify layers of each ggplot. The default horizontal axis label is “Difference” if .by_var = TRUE is specified in the plot() function.

g_0 <- plot_0 +
  coord_cartesian(xlim = c(0.2, 0.8)) +
  scale_x_continuous(breaks = c(0.3, 0.5, 0.7)) +
  theme(plot.title = element_text(hjust = 0.5)) +
  labs(title = "Non-white", 
       x = "AMCE")

g_1 <- plot_1 + 
  coord_cartesian(xlim = c(0.2, 0.8)) +
  scale_x_continuous(breaks = c(0.3, 0.5, 0.7)) +
  theme(axis.text.y = element_blank(),
        plot.title = element_text(hjust = 0.5)) +
  labs(title = "White",
       x = "AMCE")

g_d <- plot_d + 
  coord_cartesian(xlim = c(-0.4, 0.4)) +
  scale_x_continuous(breaks = c(-0.25, 0, 0.25)) +
  theme(axis.text.y = element_blank(),
        plot.title = element_text(hjust = 0.5)) +
  labs(title = "Difference")

library(patchwork)
g_0 + g_1 + g_d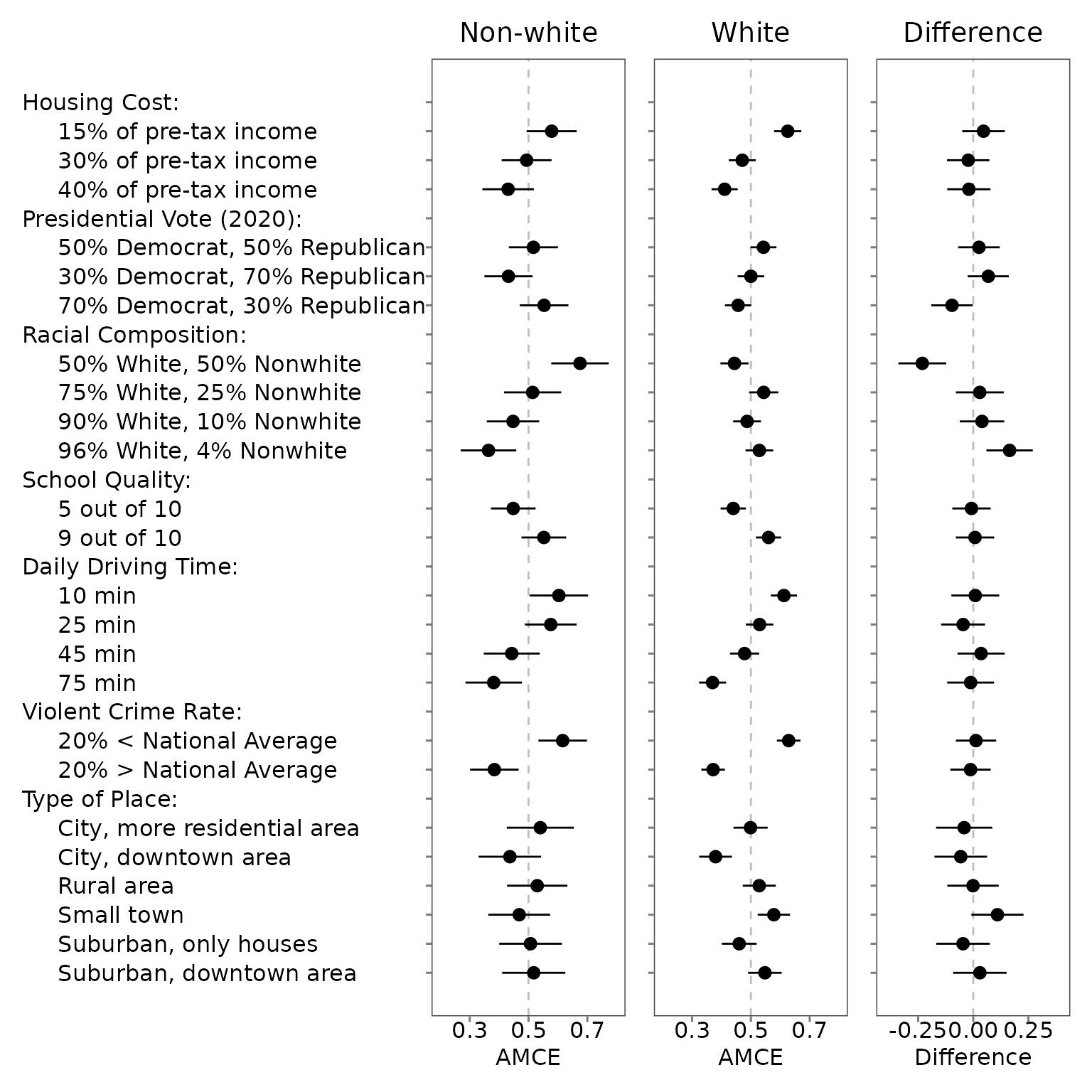

6.3 Choice-level analysis

We encourage users of our package to make custom figures based on the estimates of your choice-level analysis. The following is just one example.

df_D <- exampleData1 %>% 
  filter(party_1 == "Democrat") %>% 
  reshape_projoint(outcomes)

df_R <- exampleData1 %>% 
  filter(party_1 == "Republican") %>% 
  reshape_projoint(outcomes)

df_0 <- exampleData1 %>% 
  filter(party_1 %in% c("Something else", "Independent")) %>% 
  reshape_projoint(outcomes)

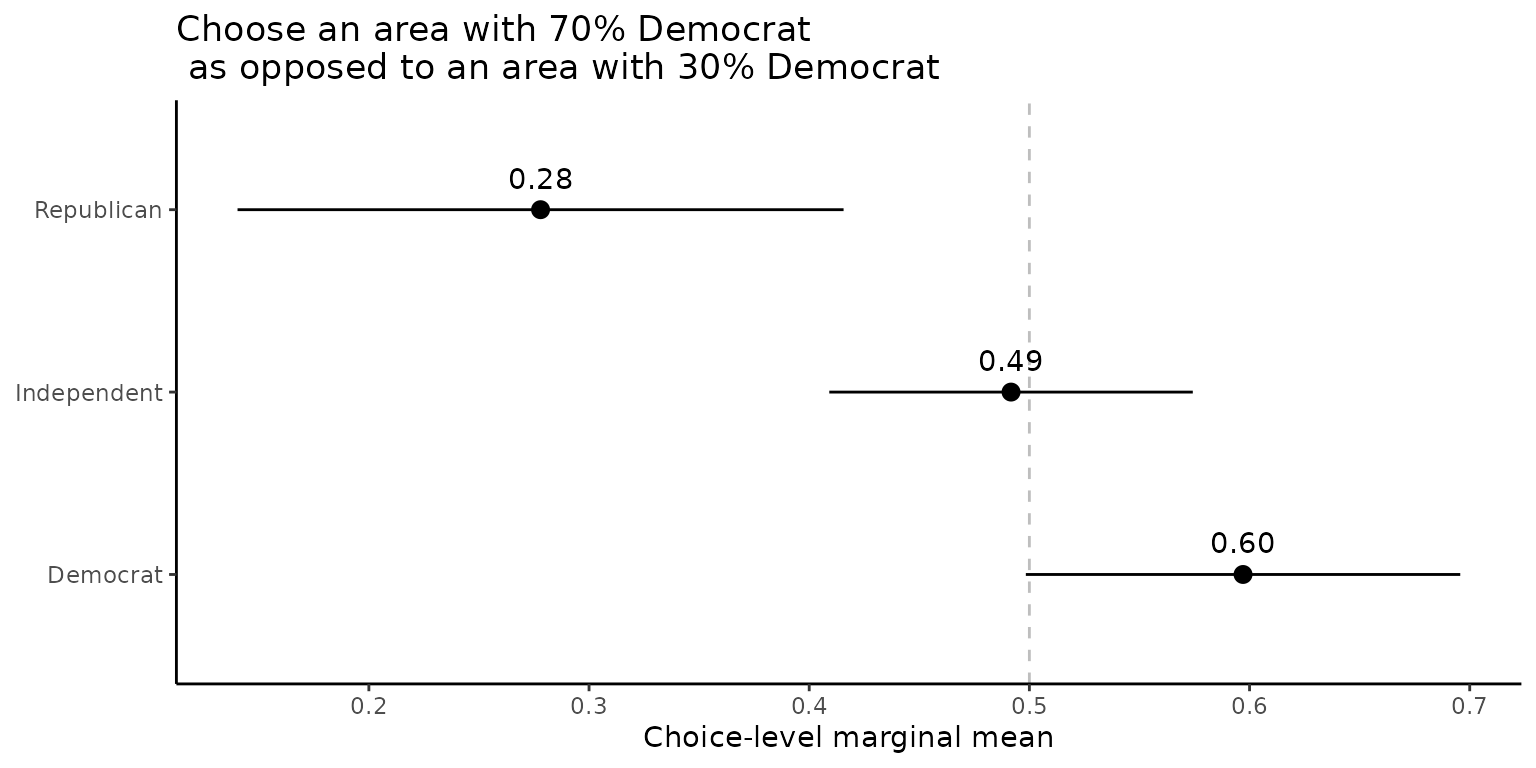
qoi <- set_qoi(
  .structure = "choice_level",
  .estimand = "mm",
  .att_choose = "att2", # Presidential Vote (2020)
  .lev_choose = "level3", # 70% Democrat, 30% Republican 
  .att_notchoose = "att2", 
  .lev_notchoose = "level1", # 30% Democrat, 70% Republican
)

out_D <- projoint(df_D, qoi)
out_R <- projoint(df_R, qoi)
out_0 <- projoint(df_0, qoi)

out_merged <- bind_rows(
  out_D@estimates %>% mutate(party = "Democrat"),
  out_R@estimates %>% mutate(party = "Republican"),
  out_0@estimates %>% mutate(party = "Independent")
) %>% 
  filter(estimand == "mm_corrected")

ggplot(out_merged, 
       aes(y = party,
           x = estimate)) +
  geom_vline(xintercept = 0.5,
             linetype = "dashed", 
             color = "gray") +
  geom_pointrange(aes(xmin = conf.low,
                      xmax = conf.high)) +
  geom_text(aes(label = format(round(estimate, digits = 2), nsmall = 2)),
            vjust = -1) +
  labs(y = NULL,
       x = "Choice-level marginal mean", 
       title = "Choose an area with 70% Democrat\n as opposed to an area with 30% Democrat") +
  theme_classic()