Estimate intra-respondent reliability (tau) without a repeated task

Uses the extrapolation method to estimate intra-respondent reliability (IRR, $\tau$) when your conjoint design does not include an explicit repeated task. The input is a projoint_data object (e.g., produced by reshape_projoint).

Usage

predict_tau(.data, .title = NULL)

Arguments

.data: A projoint_data object (from reshape_projoint).
.title: Optional character string used as the plot title prefix.

Value

A projoint_tau object (list-like) with components:

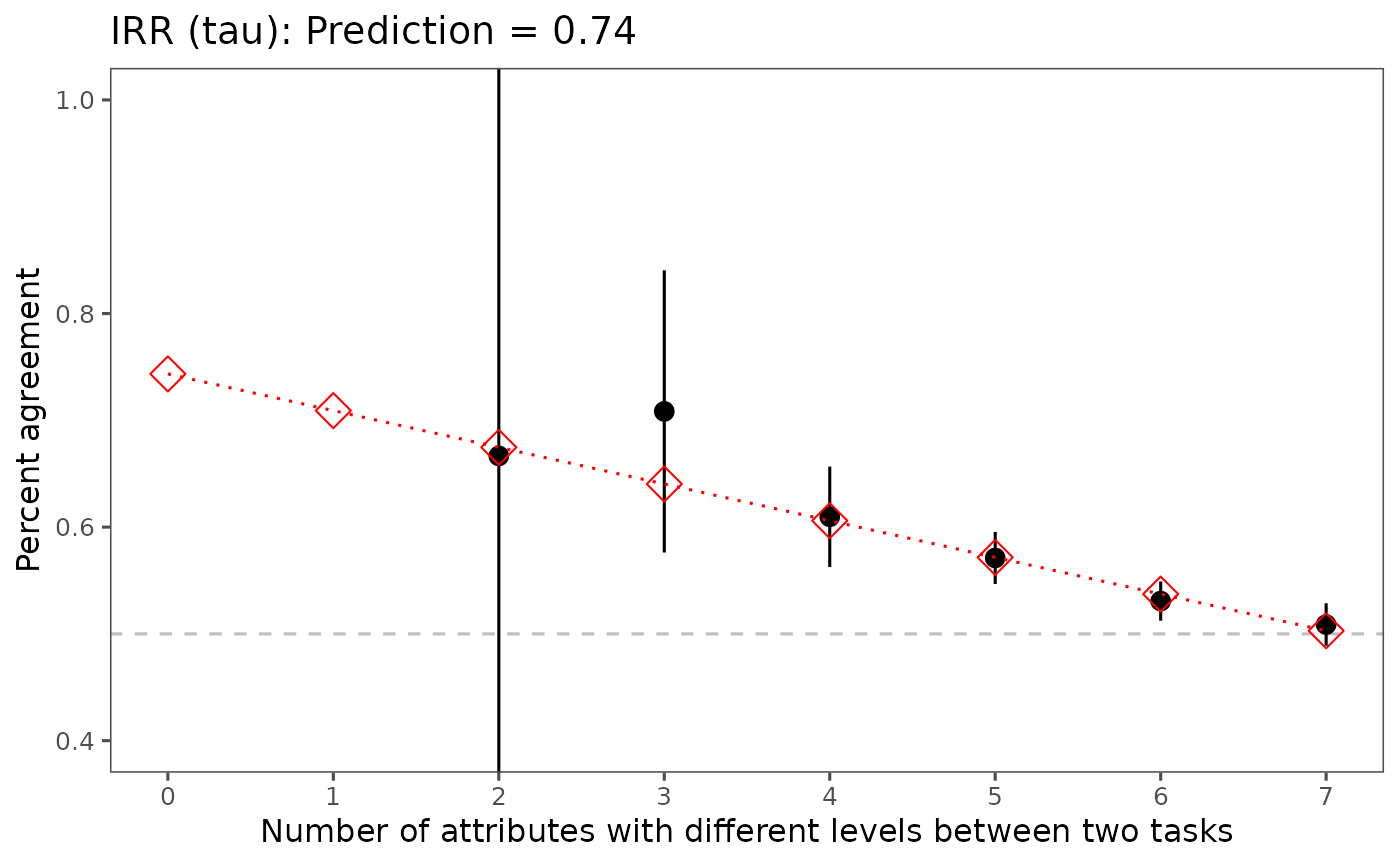
$irr: a tibble with columns x (number of differing attributes) and predicted (fitted agreement), including x = 0 which is the estimate of $\tau$.
$figure: a ggplot2 object visualizing observed agreement by x and the fitted line with the extrapolated point at x = 0.

Details

The procedure constructs pairs of base tasks within respondent, computes the proportion of identical choices as a function of how many attributes differ between the two tasks, fits a weighted regression of agreement on the number of differing attributes, and extrapolates to zero differences to obtain $\hat{\tau}$.

Examples

# \donttest{
# Example workflow:
data(exampleData1)
outcomes <- c(paste0("choice", 1:8), "choice1_repeated_flipped")

# Even if your real study lacks a repeated task, this shows the API:
pj <- reshape_projoint(exampleData1, outcomes, .repeated = TRUE)

tau_fit <- predict_tau(pj, .title = "IRR (tau): ")
# Inspect the extrapolated tau (row where x == 0)
tau_fit$irr[tau_fit$irr$x == 0, ]
#> # A tibble: 1 × 2
#>       x predicted
#>   <int>     <dbl>
#> 1     0     0.743

# Plot (also available via plot(tau_fit))
print(tau_fit$figure)

# }